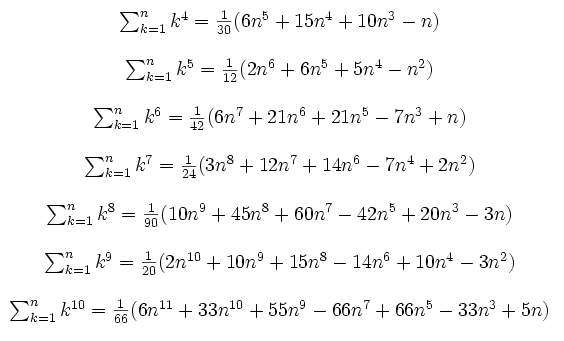Dedicato a chi si occupa di scienza
e di divulgazione scientifica.
E’ ricominciato il carnevale della Fisica, anzi addirittura ce ne sono due:
Il (non) carnevale della fisicae questa è una buona notizia.
Se dovessi scegliere una sola formula, tra le tante che si possono trovare in un libro di Fisica, avrei sicuramente l’imbarazzo della scelta.
Ma dovendo fornire una sola risposta, la scelta sarebbe:
Rµν– ½ gµνR = k Tµν
L’equazione lega la curvatura dello spazio-tempo al tensore energia-impulso che descrive la densità e il flusso di materia-energia.
I membri dell'equazione sono tensori simmetrici di dimensione 4x4, contenenti quindi 10 componenti indipendenti (sarebbero 16 se non fossero simmetrici) che variano in funzione del punto considerato.
Il membro a sinistra dell'uguaglianza misura la curvatura e la geometria dello spazio-tempo, mentre quello di destra misura la densità e il flusso di materia e energia. L'equazione descrive quindi in che modo la materia "curva" lo spazio-tempo e ne determina la geometria; a sua volta la curvatura dello spazio-tempo “determina” come la materia si muove (geodetiche).
In fisica e matematica esistono grandezze scalari (come temperatura o massa) e grandezze vettoriali (per esempio forza e velocità), però si possono anche definire oggetti geometrici, come i tensori, di ordine superiore: uno scalare è un tensore di ordine zero (senza indici), un vettore è un tensore di ordine 1 (con un indice) e allo stesso modo vengono definiti i tensori di ordine n (con n indici).
Si tratta di un sistema di 10 equazioni differenziali alle derivate parziali non lineare nelle incognite del tensore metrico.
Una volta trovata, la “metrica” si utilizza poi nella equazione geodetica del moto.
In parole più semplici, la distanza (metrica) tra due punti nello spazio-tempo risulta definita dalla distribuzione della materia (e dell’energia); questo ci permette di calcolare il cammino più breve (geodetica) che percorre un corpo in caduta libera od in orbita intorno ad un pianeta.
Einstein ebbe a dire che la parte sinistra della equazione è fatta di puro marmo pregiato e rappresenta la geometria dello spazio-tempo, mentre quella destra è fatta di volgare legno e rappresenta l’energia-materia tramite il tensore energia-impulso.
Il motivo di questa affermazione consiste nel fatto che il tensore sulla destra dell’equazione rappresenta in modo impreciso la distribuzione della materia, non tenendo conto della sua reale composizione.
L’importanza della geometria non-euclidea per lo spazio fisico cominciò a chiarirsi dopo la pubblicazione postuma del fondamentale trattato di Bernhard Riemann“Sulle ipotesi che stanno alla base della geometria”. Nella geometria euclidea vale il teorema di Pitagora, cioè utilizzando un sistema di coordinate cartesiane, per la distanza “s” di un punto dall’origine vale s2= x2 +y2
o se ci si limita a spostamenti molto piccoli (infinitesimi) che si indicano “ds” si ha:ds2= dx2 + dy2
La forma più generale per una superficie curva è invece:
ds2 = g11dx2 + 2 g12dx dy + g22dy2 = gjkdxjdxk.
Dove le gik, simmetriche in j e k , sono le componenti di un tensore che descrive le proprietà metriche (e quindi il campo gravitazionale) del sistema.
Riemann postulò la validità del teorema di Pitagora nell’infinitamente piccolo.
Utilizzando le parole di Einstein:
“Se nella teoria della Relatività Generale esiste un equazione analoga a quella di Poisson, deve trattarsi di un’equazione tensoriale per il tensore gµνdel potenziale gravitazionale; il tensore energetico della materia dovrà poi figurare in essa a secondo membro, mentre a primo membro dovrà figurare un tensore differenziale nelle gµν. Dobbiamo ora ricercare tale tensore differenziale, il quale risulta completamente determinato dalle 3 condizioni seguenti:
1) non deve contenere alcuna derivata delle gµνdi ordine superiore al secondo;
2) deve essere lineare e omogeneo nelle derivate seconde;
3) la sua divergenza deve essere identicamente nulla.
Le prime 2 condizioni sono tratte naturalmente dall’equazione di Poisson.”
La terza condizione è necessaria per poter soddisfare il principio di conservazione dell’energia.Dal tensore gµνe dalle sue derivate prime possono essere costruite delle grandezze (connessione affine) che non hanno però le caratteristiche di un tensore in quanto possono essere annullate scegliendo un opportuno sistema di riferimento. Senza entrare troppo nei dettagli, queste rappresentano il campo gravitazionale, che può venire annullato localmente scegliendo un sistema in caduta libera.
Utilizzando anche le derivate seconde Riemann riuscì a ricavare il tensore di curvatura che porta il suo nome.
Anche in questo, come nel caso della meccanica classica, non sono necessarie derivate di ordine superiore.
Come visto nel precedente post: 13. Equazioni del motola derivata prima della posizione fornisce la velocità, mentre la sua derivata seconda l’accelerazione e moltiplicando questa per la massa si arriva alla definizione di forzaF = ma
Ora dalla legge di gravitazione universale di Newton che determina la forza esercitata tra due oggetti di massa m1 ed m2 ad una certa distanza R, si riesce a ricavare l’accelerazione con la quale un oggetto modifica il proprio moto a causa di un’altra massa.
E’ infine illuminante come sia semplice la forma delle equazioni di campo di Einstein nel vuoto (che permettono di calcolare i moti di tutti gli oggetti sottoposti ad un campo gravitazionale, come proiettili o pianeti):
Rµν= 0
Credo che sia difficile trovare una formula più elegante di questa.
Per completezza riporto l’equazione di Einstein nelle due versioni e le loro corrispondenti in meccanica classica: equazioni di Poisson e di Laplace.
Con visione profetica Riemann scrisse: “Le basi della determinazione metrica devono essere cercate nelle forze di legame che agiscono su di essa”
L’anticipazione di Riemann di una dipendenza della metrica dai dati fisici, sembra sia stata la soluzione logica di un dilemma. Poiché tale curvatura è una proprietà intrinseca dello spazio, ossia può essere determinata da misure geometriche all’interno dello spazio stesso. Le indicazioni di Riemann vennero ignorate dalla maggior parte dei matematici e dei fisici suoi contemporanei. Le sue ricerche sembrarono troppo speculative e teoriche. Il solo che si accostò a Riemann fu il traduttore in inglese delle sue opere, William Kingdon Clifford. Già nel 1870 Clifford aveva visto nella concezione dello spazio di Riemann la possibilità di fondere la geometria con la fisica. Per Riemann la materia era la causa della struttura dello spazio. Clifford invece concepì la materia e il suo moto come una manifestazione del variare della curvatura. Egli suppose che la curvatura riemanniana potesse dare origine a mutamenti nella metrica del campo alla maniera delle onde, causando in tal modo increspature che potevano essere interpretate come movimento della materia. Per Aristotele lo spazio era un accidente della sostanza; per Clifford la sostanza è un accidente dello spazio.
Ma perché non si giunse subito ad una nuova teoria fisica?
Cosa mancava?
Mancava la teoria della Relatività Ristretta, ma soprattutto la visione successiva di Hermann Minkowski che con l’introduzione dello spazio-tempo come continuo quadridimensionale fornì il corretto ambito in cui sviluppare la nuova teoria. La gravitazione, come viene interpretata dalla teoria della Relatività Generale, deve essere compresa nella struttura geometrica dello spazio-tempo. Questa fusione rende la teoria in accordo (per definizione) con quanto predetto (e sperimentato) dalla Relatività Ristretta e alla spiegazione dei famosi effetti osservabili: spostamento del perielio di Mercurio, deviazione dei raggi luminosi, ecc.).
Il procedimento per giungere alla RG fu molto complesso e durò circa 10 anni. Si basa su una intuizione di Einstein del 1907: il Principio di Equivalenza. Questo permette di estendere il principio di relatività a qualsiasi osservatore in moto accelerato e porta alle equazioni che spiegano la precessione del moto del perielio di Mercurio (sebbene utilizzando approssimazioni successive e non la soluzione esatta trovata successivamente da Karl Schwarzschild). Tornato in Svizzera ne parla con l’amico e collega Marcel Grossmann e dopo qualche anno riesce a generalizzare l’equazione di Poisson per il potenziale (scalare) gravitazionale a un potenziale tensoriale gravitazionale con 10 elementi indipendenti individuati in funzione delle sorgenti energetiche del campo (il tensore energia-impulso). Nel frattempo anche David Hilbert presenta equazioni di campo corrette derivandole da un principio variazionale. Potrei continuare fornendo un esempio di soluzione dell’equazione di Einstein, ma forse è più corretto rimandare alla chiara esposizione di Wikipedia:
Dalla versione inglese di Wikipedia dello stesso argomento:
“The Schwarzschild solution is named in honor of Karl Schwarzschild, who found the exact solution in 1916, a little more than a month after the publication of Einstein's theory of general relativity. It was the first exact solution of the Einstein field equations other than the trivial flat space solution. Schwarzschild died shortly after his paper was published, as a result of a disease he contracted while serving in the German army during World War I.”
Aneddoto:
uno dei libri che ho sempre considerato fonte inesauribile per quanto riguarda la Teoria dei Campi ed in particolare della teoria della Relatività Generale e’:
L. D. Landau – E. M. Lifsits, TEORIA DEI CAMPI (Nuova biblioteca di cultura scientifica)
Al secondo anno di università’ incontrai in metropolitana un ex compagno delle superiori, che, alla vista del libro sopra menzionato che portavo spesso con me, fece l’affermazione:
“vedo che ti sei iscritto alla facoltà di Agraria”
Albert Einstein, Il significato della relatività, Ed. Bollati Boringhieri
Albert Einstein, Opere scelte, a cura di E. Bellone, Ed. Bollati BoringhieriMax Jammer, Storia del concetto di spazio, Ed. FeltrinelliSteven Weinberg, Gravitation and Cosmology, Ed. J.Wileyhttp://zibalsc.blogspot.it/2014/03/143-curvatura-e-gravitazione.htmlhttp://zibalsc.blogspot.it/2013/06/123-paradosso-dei-gemelli-bis.html